The Library and Lighthouse of Alexandria

Alexandria became the undisputed center of mathematics in the ancient world. This was because it had the best numbers.

In order to write about something, in order even to think about it properly, we must have symbols for representing it. Our modern set of numerical symbols and the method of counting they enable is known as the Hindu-Arabic numeral system. It has become so ingrained in our consciousnesses that it now seems inseparable from the abstract idea of mathematics itself. It has become ubiquitous all over the world, across cavernous gulfs in language and culture, simply because it works better than any of the alternatives. But it took us a long, long time to arrive at this point. The familiar numerals of today are far younger than the city of Alexandria, much less mathematics in general. They started to become the standard around the world only in the fifteenth century AD, when they became one of the greatest of the many gifts which the Muslim nations bestowed upon their Christian counterparts at the dawn of the Renaissance.

Before that, people had to make do with other, less convenient number systems. One of the systems they used is still familiar to us. The so-called “Roman numerals” that we employ to lend a note of extra interest and gravitas to our sporting events and blockbuster movie sequels were indeed the principal counting tools of the ancient Romans. Personally, I enjoy them in an odd sort of way; decoding a long string of them is like solving a little cryptogram. But they’re anything but optimal tools for complex calculation.

Long before the Romans, the Egyptians employed a system that was conceptually similar. A hieroglyph of a lotus flower (𓆼) stood for 1000, a snare (𓍢) for 100, an inverted wicket (𓎆) for ten, and a single vertical stroke — not that dissimilar from our modern singular numeral — stood for one. So, the number 2342 looked like this:

𓆼𓆼𓍢𓍢𓍢𓎆𓎆𓎆𓎆𓏺𓏺

It was the Mesopotamians who invented what’s known as “positional notation”: a system whereby each symbol is multiplied by an increasing power of a base value as you move from right to left. But, whereas our modern number system uses a base value of ten, the Mesopotamians chose a base value of 60. They wrote the number 2342 like this:

𒌍𒐝  𒐖

The right-hand symbol above represents (2 * 60⁰), or simply two; the physically wider left-hand symbol represents (39 * 60¹), or 2340. One adds the values of the positions together to arrive at a final value, just as we do in our number system of today.

We still encounter a lingering vestige of this first positional number system every day, in the form of our division of a minute into 60 seconds and an hour into 60 minutes. Still, a base 60 number system proves less than ideal for calculation; 60 are just too many base values for the average person to comfortably hold in the mind when attempting to learn multiplication tables and the like.

Perhaps a century before the founding of Alexandria, perhaps a little earlier, the Greeks devised an alternative positional number system based on ten, a value which seemed to suit the human mind perfectly. Indeed, this Greek system would remain the best, most practical example of its kind right through the remainder of classical times. It was based upon the Greek alphabet: alpha (α) stood for one, beta (β) for two, etc. It was different from our modern system, however, in that it lacked a symbol for zero to serve as a placeholder in “empty” positions. Thus it had to use unique symbols in every position; otherwise there would be no way to distinguish the number 25 from 205. (Suffering from the same lack of a zero placeholder, the Mesopotamians had tried to insert spaces where “missing” digits ought to go. Combined with the inherent imprecision of carving letters onto clay tablets, the approach has played havoc with our ability to decipher their numbers accurately today. It was probably responsible for no small degree of confusion even in ancient times.)

The Greek alphabet as it existed after about 500 BC had just 24 letters, so three obsolete letters were reintroduced to complete a set of 27 symbols, sufficient to represent any number up to 999. Powers of 1000 reused the first nine letters of the alphabet, but preceded them with a mark to point out their change in value. Thus the number 2342 would be written like this:

,βτμβ

Reading from right to left here, we have the Greek letter beta, representing two; mu for 40; and tau for 300. Finally, beta does double duty to represent 2000.

Fractions, which most earlier number systems had handled poorly if at all, could be written with relative ease in the Greek system by drawing a horizontal bar over the numerator, then making a mark after the denominator. So, 23.42 would appear as “23 42 100,” when transliterated into our number system. Or, in the Greek:

κγ μβ ρ,

There was no agreed-upon way to write numbers larger than 9999, an issue to which I’ll return later. For now, I will note only that the ancients generally had less need of such large values than we do today.

A man named Euclid made good use of the innovations just described. He was most definitely not the first Greek mathematician — “Let no one ignorant of mathematics enter here” was written on the pediment of Plato’s school in Athens already by 380 BC, while Pythagoras formulated the famous theorem which still bears his name well over a century before that — but he was perhaps the most important; in fact, he would become arguably the most important mathematician in the entire history of the world, so much so that he is sometimes given the title of “Father of Mathematics.” And, for a time at least, he did his work from Alexandria.

We know almost nothing about the man himself. We can surmise that he was probably born around 325 BC and died around 265 BC, but even that is no more than a best guess. We don’t even know where he was born or where he died. The merest whiff of a trace of his life can be found in the writings of Proclus, a Greek philosopher and historian who lived some 750 years after him. He tells us that Euclid synthesized the work of various earlier mathematicians into the scintillating whole known as the Elements of Geometry, and that he was active in Alexandria at a very early date: “in the time of the first Ptolemy.” Proclus also shares a personal anecdote from Euclid’s life, one of only two that we have. It seems that Ptolemy I asked him if there wasn’t a shorter way to an understanding of geometry than reading through the Elements, a work of considerable heft. “There is no royal road to geometry,” answered Euclid.

The other anecdote stems from a source even farther removed in time from Euclid than Proclus was; it comes from the fifth century AD, from a book of quotations deemed useful for moral instruction. Therein a precocious student asks Euclid what he stands to gain by studying mathematics. In reply, Euclid promises him a few coins if he finishes his course, “since he must needs make gain of what he learns.”

These two gently witty rebukes will have to suffice for us as we try to paint a picture of Euclid in our mind’s eye. Otherwise, we have only his masterwork the Elements, which has come down to us largely intact. It is certainly enough of a legacy for anyone.

Euclid’s Elements has been called the most influential book in the history of the world, excepting only the Bible. It is undoubtedly the most timeless book of practical instruction ever written. To this day it remains the bedrock of the field of mathematics that bears Euclid’s name: that of Euclidian geometry. When we use that phrase, we actually mean all geometry as it existed until the nineteenth century AD, the geometry which is still the only one known to all but advanced students of higher mathematics today. Architects and construction managers, cartographers and videogame programmers rely upon the Elements to do their work, whether they’re aware of it or not. Johannes Kepler used it to develop his laws of planetary motion; NASA engineers used it to plot a manned space capsule’s course to the Moon and back.

Just as important as the practical information contained in the Elements is the new way of doing mathematics that it heralded. If, as Proclus believed, its raw information was not entirely or perhaps even primarily original to the book’s author, but was rather a synthesis of older ideas from thinkers such as Pythagoras, its structure alone is still enough to certify Euclid’s claim to genius. For he was the first mathematician that we know of to employ what we call the axiomatic approach. This means that he begins with a set of primitive axioms — truths which are so basic and self-evident that they cannot be broken down into more granular logical proofs — and then uses them as the foundation for a grander edifice of logic. This is still the way that mathematics is done today, thus justifying those who wish to call Euclid the “Father” of that discipline.

Euclid assumes nothing later on that he doesn’t clearly state at the start of his work, where he defines two-dimensional geometric space at its most fundamental.

• A point is that which has position but not dimension.
• A line is length without breadth.
• The intersections of lines and their extremities are points.
• A line which lies evenly between its extreme points is called a straight or right line.
• A surface is that which has length and breadth.
• When a surface is such that the right line joining any two arbitrary points in it lies wholly in the surface, it is called a plane.
• When one line stands on another, and makes the adjacent angles at both sides of itself equal, each of the angles is called a right angle, and the line which stands on the other is called perpendicular to it.
• A triangle is a figure formed by three right lines joined end to end. The three lines are called its sides.
• A triangle whose three sides are unequal is said to be scalene; a triangle having two sides equal, to be isosceles; and having all its sides equal, to be equilateral.
• A circle is a plane figure formed by a curved line called the circumference, and is such that all right lines drawn from a certain point within the figure to the circumference are equal to one another. This point is called the center.

From definitions like these, he proceeds to a series of “propositions,” more complex methods and rules that can be deduced from the simpler truths.

• If two triangles have two sides of one equal respectively to two sides of the other, and have also the angles included by those sides equal, the triangles shall be equal in every respect.
• The angles at the base of an isosceles triangle are equal to one another, and if the equal sides be produced, the external angles below the base shall be equal.

The proofs which Euclid goes on to provide for his propositions are the first of their type in the preserved canon of ancient mathematics. By the end of the book, he has progressed from simple concepts like the ones above to higher number theory, including the irrational numbers and proportions, and three-dimensional (or solid) geometry to complement his two-dimensional points, lines, and shapes.

Forget for a moment its practical value; in the hands of the right reader, Euclid’s Elements can be as moving as any great work of literature. Plato seemed to anticipate its splendor when he wrote that “the knowledge of which geometry aims is the knowledge of the eternal.” Looking back upon it, Will Durant called the Elements “a mathematical architecture that rivaled the Parthenon as a symbol of the Greek mind.” Following Euclid’s methodical progress from first principles to glorious complexity can be a profound spiritual experience, as the language some use to describe it well shows. Bertrand Russell wrote that “at the age of eleven, I began Euclid. This was one of the great events of my life, as dazzling as a first love. I had not imagined that there was anything so delicious in the world.” Edna St. Vincent Millay wrote that “Euclid alone has looked on Beauty bare.”

We don’t know how long Euclid lived in Alexandria. But we do know that his way of orienting himself to the world — an orientation based on observed phenomena rather than received faith — became the Alexandrian way. The city’s justifiably vaunted intellectual tradition was built upon his example of rigorous reasoning from first principles, as applied not only to mathematics but to many other fields besides. Many a brilliant mind would live in Alexandria after him, but none of them would be more important in the grand scheme of things.

That said, some of them definitely did come close. One of these was a mathematician and proto-scientist named Archimedes, about whom we know a little bit more than we do of Euclid.

Archimedes was born in or around 287 BC in Syracuse, an independent Greek city-state on the island of Sicily. His father was a wealthy member of the city’s ruling class. The son had no interest in politics, but did show exceptional talent in many intellectual fields, especially mathematics. He was likely still a teenager when he sailed across the Mediterranean Sea to join the museum in Alexandria. He probably arrived there a little too late to meet Euclid, but the man’s spirit must have been in the air, if you will. Archimedes became in many ways the heir to his achievements, quickly collecting a following of his own that belied his tender age. Folklore tells of him wandering along the beach in deep conversation with his disciples, stopping from time to time to scratch numbers and diagrams into the sand with sticks in order to illustrate a point.

Archimedes’s ideas, whether expressed verbally or on the page, led to many practical inventions. The compound pulley he conceived for the purpose of loading and unloading ships remains a staple of modern life; if you don’t wish to go down to a harbor to see one in action, you can just visit your local auto shop and observe their engine lift. (“Give me another world to stand upon, and I will move this upon which we live,” he said famously if apocryphally.) And he appears to have invented the world’s first serviceable odometer, which would later be used to wonderful effect by the Romans as they laid out the finest road network ever to exist in the world prior to the last couple of centuries of our era.

For all that, though, Archimedes was a theorist at heart, content to let others do the vaguely distasteful work of turning his words, numbers, and diagrams into such practical tools. Meanwhile he turned his attention to yet more airy abstractions.

Indeed, Archimedes is something of a prototype for the assorted genius innocents of modern reality and pop culture, so obsessed with their intellectual pursuits as to have trouble engaging with the real world. Plutarch tells how Archimedes’s mind never stopped working even when he was on the receiving end of a sensuous massage:

He seemed ever bewitched by the song of some indwelling siren of his own so as to forget to eat his food, and to neglect his person. When dragged forcibly to the baths and perfumers, he would draw geometrical figures with the ashes on the hearth, and when his body was anointed would trace lines on it with his finger, absolutely possessed and inspired by the joy he felt in his art.

Archimedes decided at one point that he wanted to figure out how many grains of sand would fit into the universe. The first problem he had to solve in order to do so was one of representation: the Greek number system he was using, you’ll remember, only extended as far as 9999. Any number beyond that was described simply as a “myriad.” So, Archimedes devised a “myriad notation” for representing these higher numbers. When the Greek letter mu followed a set of one to four digits, it indicated that said digits constituted a myriad, which was to be multiplied by 10,000 to determine its value. The myriad might then be followed by another series of digits denoting the last four positions of the complete number. Thus the number 22,342 would look like this (note that the Greek letter mu looks like our alphabet’s “M”):

βM,βτμβ

Myriad notation made it possible to write values up to and including 99,999,999. But even that wouldn’t suffice for counting every grain of sand in the universe. Therefore Archimedes invented a system of writing truly enormous numbers when pinpoint accuracy is not required — a system that’s similar in the broad strokes to our modern scientific notation. It could be used to count myriads of myriads, or myriads of myriads of myriads, or… you get the picture. The highest number Archimedes imagined representing in this way would have to be written in modern traditional notation as a one followed by one quadrillion zeroes — quite a leap indeed from the old limit of 9999. This work would prove foundational to the invention of logarithms much later.

Archimedes used his new system to write that it would take 10⁶³ grains of sand to fill the universe. We’ll return to the question of how he arrived at that figure in the next chapter, when we delve into Alexandrian astronomy.

For now, though, so much for large numbers. In the realm of smaller ones, Archimedes expanded upon the work of Euclid by calculating a more exact value for pi, that necessary ratio between a perfect circle’s circumference and its diameter. Prior to him, the Egyptians had concluded that this value was 3.16, the Mesopotamians 3.13. But Archimedes now honed in on it with much more precision.

The calculation of a ratio between two existing numbers was trivial enough; the endeavor of calculating pi was made difficult only by the impossibility of measuring precisely along the curve of a circle’s circumference in order to determine what one of the two numbers should be. Archimedes came up with a typically ingenious method of doing so with a finer degree of precision than anyone before him had managed. He drew a perfect hexagon just inside of a perfect circle, and another hexagon just outside of it, then measured the perimeter of each hexagon. He knew that the correct circumference of the circle must lie between these two numbers. Having come this far, he repeated the process with twelve-sided polygons, then 24-sided, then 48-sided, and finally 96-sided. His method was later given a thoroughly appropriate name: “The Method of Exhaustion.” In the end, he concluded that pi was between 3.141 and 3.143. As it happens, the real number rounded to three decimal places is 3.142; Archimedes’s approximation was as spot-on as it could reasonably be. Generations to come would be in his debt for making their calculations that much more accurate. (We now know, of course, that an approximation of pi is the only thing possible; it is an irrational number, meaning it continues to an infinite number of decimal places without ever stopping or revealing a pattern.)

Archimedes was also fascinated with spirals, those oddly beautiful three-dimensional forms that occur again and again in nature. One suspects he would have agreed with Vladimir Nabokov when the latter called the spiral “a spiritualized circle. In the spiral form, the circle, uncoiled, unwound, has ceased to be vicious; it has been set free.” Spirals look like they’re moving even when they’re sitting still. When we think of them, a presumption of motion always seems to come attached: the rotation of the grooves of a record, the curl of a fern tendril moving in the breeze, the unfurling of a scroll, the explosive expansion of a tightly wound spring, the slow unwinding of a spiral galaxy.

Archimedes’s study of spirals is suitably dynamic. In contrast to the “essentially static” nature of most Greek mathematics, write Uta C. Merzbach and Carl B. Boyer in their History of Mathematics, Archimedes displays “kinetic considerations akin to differential calculus” when he turns to the subject of spirals. This work led directly to his most famous invention of all: the screw pump, a rotating spiral inside a cylinder sitting half in, half out of the water. It was used in ancient times to irrigate fields and to pump bilge water out of ships, and is still used for those purposes and many others today. (It is possible, even likely, that Archimedes found the screw pump already in use for irrigation in Egypt when he arrived there; it may also have already been in use in Mesopotamia. But even if so, his documentation of the contraption served to spread it far and wide, as well as explicating the principles that caused it to work in the first place.)

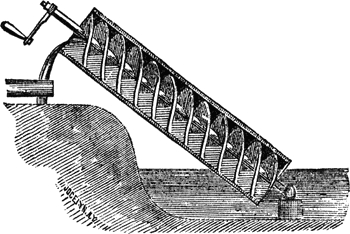
There is much, much more to Archimedes than I can describe in any detail here. For example, his experiments with centers of gravity laid the groundwork for the theories of Isaac Newton, and his work with buoyancy yielded formulas that are still used by scientists today.

If we had access to everything Archimedes wrote, we would doubtless rush to label him even more of a genius. We know that in the field of three-dimensional geometry, for instance, he discovered all thirteen of the possible semi-regular solids, objects whose faces are composed of more than one kind of regular polygon arranged in a repeating pattern; think of the twenty hexagonal and twelve pentagonal faces of a soccer ball. But we know of his discoveries in this area only from the reports of later writers; his original texts in this vein are lost. Not until AD 1619 would Johannes Kepler rediscover the last of the thirteen solids which Archimedes had described almost two millennia earlier.

We know as well that Archimedes had an endearing fondness for puzzles and jokes. One vivid illustration of his playful side came to light only in AD 2003, on an ancient manuscript of his which was overwritten by monks during Medieval times but finally recovered with the aid of modern imaging technology. It deals with the Stomachion, a toy consisting of fourteen flat cut-out shapes inside a rectangular frame. It seems to have served as a sort of ancient version of Legos; children could combine the shapes together to create pictures and designs. But, more interestingly for Archimedes, Stomachion was also a form of puzzle; when one was finished playing with it, one had to figure out how to fit all of the shapes back into the frame. Archimedes set out to determine how many different ways there were of doing so with the same level of dedication which he applied to any of his other projects; in doing so, he anticipated the modern mathematical field of combinatorics. But the manuscript in question is unfortunately incomplete, cutting off well before he reveals his final conclusion. (By making liberal use of computers, modern mathematicians have determined that there are 17,152 possible combinations in all.)

During Archimedes’s later years, another brilliant mathematician’s star began to rise in Alexandria. Apollonius came there from Perga, a Greek settlement on what is today the southwestern coast of Turkey, at some time around 220 BC. He might be as well-remembered as Archimedes today if only more of his corpus had survived. But, in contrast to the ten full-length treatises and assorted other fragments by Archimedes that have reached us, we have just two of the texts of Apollonius. The one on conic sections is as important to the history of mathematics as any single extant work of Archimedes. Otherwise, we have only tantalizing hints of Apollonius’s genius.

The vagaries of chance have thus consigned him to being remembered as a specialist in conic sections and as the antagonist of Archimedes. Theirs was, if the stories are to be believed, a classic conflict between a wizened master and a young upstart. Apollonius dared to claim he could improve upon his better’s work via such means as the invention of his own, allegedly more efficient way of writing very large numbers; this treatise of his is one of those that are lost to us, preventing us from passing any judgments on the worthiness of his alternative method. At last, Archimedes challenged Apollonius to a showdown, mathematician-style: he sent him a puzzle to solve.

Number the sun god’s cattle, my friend, with perfect precision. Reckon them up with great care, if any wisdom you’d claim. How many cattle were there that once did graze in the meadows on the Sicilian isle, sorted by herds into four, each of these four herds differently colored? The first herd was milk white, whereas the second gleamed in a deep ebony black. Brown was the third group, the fourth was spotted.

In every division, bulls of respective hews outnumbered the cows. Now, these were the proportions among the cattle: the white ones equaled the number of brown, adding to that the third part plus one-half of the ebony cattle all taken together. Further the group of the black equaled one-fourth of the flecked plus one-fifth of them, taken along with the total of brown ones. Finally, you must assume, friend, that the total with spots equaled a sixth plus a seventh part of the herd of white cattle, adding to that the entire herd of the brown-colored kine.

Yet quite different proportions held for the female contingent: cows with white-colored hair equaled in number one-third plus one-fourth of the black-hued cattle, the males and the females. Further, the cows colored black totaled in number one-fourth plus one-fifth of the whole spotted herd, in this computation counting in each spotted cow, each spotted bull in the group. Likewise, the spotted cows comprised the fifth and the sixth part out of the total of brown cattle that went out to graze. Lastly, the cows colored brown made up a sixth and a seventh out of the white-coated herd, female and male ones alike.

If, my friend, you can tell me exactly what was the number gathered together there then, also the accurate count color by color of every well-nourished male and each female, then with right you’ll be called skillful in keeping accounts.

The above puzzle, one of several extant versions of what’s become known as Archimedes’s “cattle problem,” requires 50,389,082 cattle in all. I leave it as an exercise to readers skilled in mathematics to discover the quantity of each type and sex of cow. History does not record whether Apollonius was able to do the same.

The rivalry between Archimedes and Apollonius was quite possibly a long-distance one; the two men might very well never have met one another in person. For we know that Archimedes returned to his native Syracuse before the end of his life; we just don’t know how long before. In fact, it is in Syracuse that the most famous of all the stories of Archimedes takes place. Although it isn’t, strictly speaking, a story of Alexandria, no description of the man’s life would be complete without it.

It seems that the king of Syracuse had ordered a goldsmith to make a new crown for him, providing his subject with an ample chunk of raw gold for the purpose. But when the crown was delivered, the king grew suspicious that the man may have alloyed some of the gold with a quantity of silver before making it, keeping the rest of the more valuable metal for himself. The king asked Archimedes to test the truth of this proposition.

Even Archimedes’s prodigious intellect was stymied by the request for quite some time. To be sure, scales did exist that could weigh the crown with a high degree of accuracy, and these showed that it did indeed weigh exactly as much as the chunk of raw gold which the king had given to the goldsmith. Yet this proved nothing in itself; if the man truly had alloyed the gold with silver, he too could have used a scale to make sure the finished crown weighed just the right amount.

Steeling himself to disappoint his king — a dangerous thing for even an acknowledged great man like himself to do — Archimedes took a long bath to calm his nerves. Sinking down into the water with a sigh, he noticed how its level rose in the basin as part of it was displaced by his own body. And just like that, his mind was off and running again. Earlier experiments had taught him that the volume and weight of every pure metal as well as every alloy have a different ratio to one another. (Scientists understand today that this is because every material has a different density.) Now, he realized in a flash of insight that he could compare the volumes of the crown and of another hunk of pure gold of the exact same weight by dropping them one at a time into the same container of water and recording how much the water level rose as a result. Legend says that Archimedes was so excited that he jumped out of his bath to run naked through the streets of Syracuse, shouting “Eureka! Eureka!”: “I’ve got it!” I’ve got it!”

His method soon proved that the goldsmith really had attempted to cheat the king; the crown displaced more water than it ought to have because of the silver with which its gold was alloyed. (For good measure, he also tested a chunk of pure silver of the same weight, and found that it displaced more water than either of the other objects because its density was yet less than that of a gold-and-silver alloy.) The fate of the crooked goldsmith is not recorded in the legend, but we can assume that it was an unpleasant one.

Syracuse was in a precarious position during these latter years of Archimedes; the genteel old city found itself sandwiched between the aggressive young city-states of Carthage and Rome. Ancient historians tell us that a sense of patriotic duty compelled Archimedes to help with the defense of his city, despite his longstanding distaste for such practical work. He supposedly designed catapults that could rain boulders upon besiegers from inside the city’s walls, machines that could discharge showers of arrows all at once, even long iron claws that could drop boulders onto enemy ships in the harbor, or grab onto them and either smash them to pieces or capsize them. Still more fanciful accounts claim that he designed giant mirrors to magnify the rays of the sun and concentrate them upon enemy ships like a laser gun, incinerating them. (Shades of a similar legend about the Lighthouse of Alexandria… the two stories might well stem from the same long-forgotten root.) Plutarch states that “Archimedes had so great a mind and such immense philosophic speculations that although by inventing these engines he had acquired the glory of a more than human intellect, he would not condescend to leave behind him any writings upon the subject.” If this strikes you as perhaps a bit too convenient, you’re not alone.

Despite whatever contributions Archimedes really did make to the defense of Syracuse, the city fell to a Roman army led by a general named Marcellus in 212 BC, when its most learned resident was 75 years old. Plutarch provides three different versions of his death at the Roman soldiers’ hands, all of them doubling down on the portrait of Archimedes as a naïve innocent in a corrupted world, completely devoted to his muse of Knowledge in the abstract:

Archimedes was then, as fate would have it, intent upon working out some problem by a diagram, and having fixed his mind and his eyes alike upon the subject of his speculation, he never noticed the incursion of the Romans, nor that the city was taken. In this transport of study and contemplation, a soldier, unexpectedly coming up to him, commanded him to follow him to Marcellus; which he declining to do before he had worked out his problem to a demonstration, the soldier, enraged, drew his sword and ran him through. Others write that a Roman soldier, running upon him with a drawn sword, offered to kill him; and that Archimedes, looking back, earnestly besought him to hold his hand a little while, that he might not leave what he was then at work upon inconclusive and imperfect; but the soldier, nothing moved by his entreaty, instantly killed him. Others again relate that, as Archimedes was carrying mathematical instruments, dials, spheres, and angles, by which the magnitude of the sun might be measured to the sight, some soldiers seeing him, and thinking that he carried gold in a vessel, slew him.

---

Did you enjoy this chapter? If so, please think about pitching in to help me make many more like it. Pledge any amount you like on Patreon.

(A full listing of print and online sources used will follow the final article in this series.)